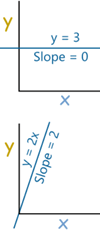Derivative Rules

(toc) #title=(Table of Content)

The Derivative tells us the slope of a function at any point.

There are rules we can follow to find many derivatives. For example:

• The slope of a constant value (like 3) is always 0
• The slope of a line like 2x is 2, or 3x is 3 etc
• and so on.

Here are useful rules to help you work out the derivatives of many functions (with examples below). Note: the little mark ’ means "Derivative of".

Common Functions	Function	Derivative
Constant	c	0
Line	x	1
	ax	a
Square	x2	2x
Square Root	√x	(½)x-½
Exponential	ex	ex
	ax	ln(a) ax
Logarithms	ln(x)	1/x
	loga(x)	1 / (x ln(a))
Trigonometry (x is in radians)	sin(x)	cos(x)
	cos(x)	−sin(x)
	tan(x)	sec2(x)
Inverse Trigonometry	sin-1(x)	1/√(1−x2)
	cos-1(x)	−1/√(1−x2)
	tan-1(x)	1/(1+x2)
Rules	Function	Derivative
Multiplication by constant	cf	cf’
Power Rule	xn	nxn−1
Sum Rule	f + g	f’ + g’
Difference Rule	f - g	f’ − g’
Product Rule	fg	f g’ + f’ g
Quotient Rule	f/g	(f’ g − g’ f )/g2
Reciprocal Rule	1/f	−f’/f2
Chain Rule (as "Composition of Functions")	f º g	(f’ º g) × g’
Chain Rule (using ’ )	f(g(x))	f’(g(x))g’(x)
Chain Rule (using ddx )	dydx = dydududx

"The derivative of" is also written ddx

So ddxsin(x) and sin(x)’ are the same thing, just written differently

Examples

Example: what is the derivative of sin(x) ?

From the table above it is listed as being cos(x)

It can be written as:

sin(x) = cos(x)

Or:

sin(x)’ = cos(x)

Power Rule

Example: What is x³ ?

The question is asking "what is the derivative of x³?"

We can use the Power Rule, where n=3:

xⁿ = nxⁿ⁻¹

x³ = 3x³⁻¹ = 3x²

Example: What is (1/x) ?

1/x is also x^-1

We can use the Power Rule, where n = −1:

xⁿ = nxⁿ⁻¹

x⁻¹ = −1x⁻¹⁻¹ = −x⁻²

Multiplication by constant

Example: What is 5x³ ?

the derivative of cf = cf’

the derivative of 5f = 5f’

We know (from the Power Rule):

x³ = 3x³⁻¹ = 3x²

So:

5x³ = 5x³ = 5 × 3x² = 15x²

Sum Rule

Example: What is the derivative of x²+x³ ?

The Sum Rule says:

the derivative of f + g = f’ + g’

So we can work out each derivative separately and then add them.

Using the Power Rule:

• x² = 2x
• x³ = 3x²

And so:

the derivative of x² + x³ = 2x + 3x²

Difference Rule

It doesn't have to be x, we can differentiate with respect to, for example, v:

Example: What is 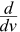(v³−v⁴) ?

The Difference Rule says

the derivative of f − g = f’ − g’

So we can work out each derivative separately and then subtract them.

Using the Power Rule:

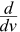• v³ = 3v²
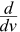• v⁴ = 4v³

And so:

the derivative of v³ − v⁴ = 3v² − 4v³

Sum, Difference, Constant Multiplication And Power Rules

Example: What is 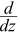(5z² + z³ − 7z⁴) ?

Using the Power Rule:

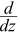• z² = 2z
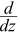• z³ = 3z²
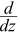• z⁴ = 4z³

And so:

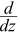
(5z² + z³ − 7z⁴) = 5 × 2z + 3z² − 7 × 4z³ = 10z + 3z² − 28z³

Product Rule

Example: What is the derivative of cos(x)sin(x) ?

The Product Rule says:

the derivative of fg = f g’ + f’ g

In our case:

• f = cos
• g = sin

We know (from the table above):

• cos(x) = −sin(x)
• sin(x) = cos(x)

So:

the derivative of cos(x)sin(x) = cos(x)cos(x) − sin(x)sin(x)

= cos²(x) − sin²(x)

 

Reciprocal Rule

Example: What is (1/x) ?

The Reciprocal Rule says:

the derivative of 1/f = −f’/f²

With f(x)= x, we know that f’(x) = 1

So:

the derivative of 1/x = −1/x²

Which is the same result we got above using the Power Rule.

Chain Rule

Example: What is ddxsin(x²) ?

sin(x²) is made up of sin() and x²:

• f(g) = sin(g)
• g(x) = x²

The Chain Rule says:

the derivative of f(g(x)) = f'(g(x))g'(x)

The individual derivatives are:

• f'(g) = cos(g)
• g'(x) = 2x

So:

ddxsin(x²) = cos(g(x)) (2x)

= 2x cos(x²)

Another way of writing the Chain Rule is: dydx = dydududx

Let's do the previous example again using that formula:

Example: What is ddxsin(x²) ?

dydx = dydududx

Have u = x², so y = sin(u):

ddx sin(x²) = ddusin(u)ddxx²

Differentiate each:

ddx sin(x²) = cos(u) (2x)

Substitue back u = x² and simplify:

ddx sin(x²) = 2x cos(x²)

Same result as before (thank goodness!)

Another couple of examples of the Chain Rule:

Example: What is (1/cos(x)) ?

1/cos(x) is made up of 1/g and cos():

• f(g) = 1/g
• g(x) = cos(x)

The Chain Rule says:

the derivative of f(g(x)) = f’(g(x))g’(x)

The individual derivatives are:

• f'(g) = −1/(g²)
• g'(x) = −sin(x)

So:

(1/cos(x))’ = −1/(g(x))² × −sin(x)

= sin(x)/cos²(x)

Note: sin(x)/cos²(x) is also tan(x)/cos(x), or many other forms.

Example: What is (5x−2)³ ?

The Chain Rule says:

the derivative of f(g(x)) = f’(g(x))g’(x)

(5x-2)³ is made up of g³ and 5x-2:

• f(g) = g³
• g(x) = 5x−2

The individual derivatives are:

• f'(g) = 3g² (by the Power Rule)
• g'(x) = 5

So:

(5x−2)³ = 3g(x)² × 5 = 15(5x−2)²